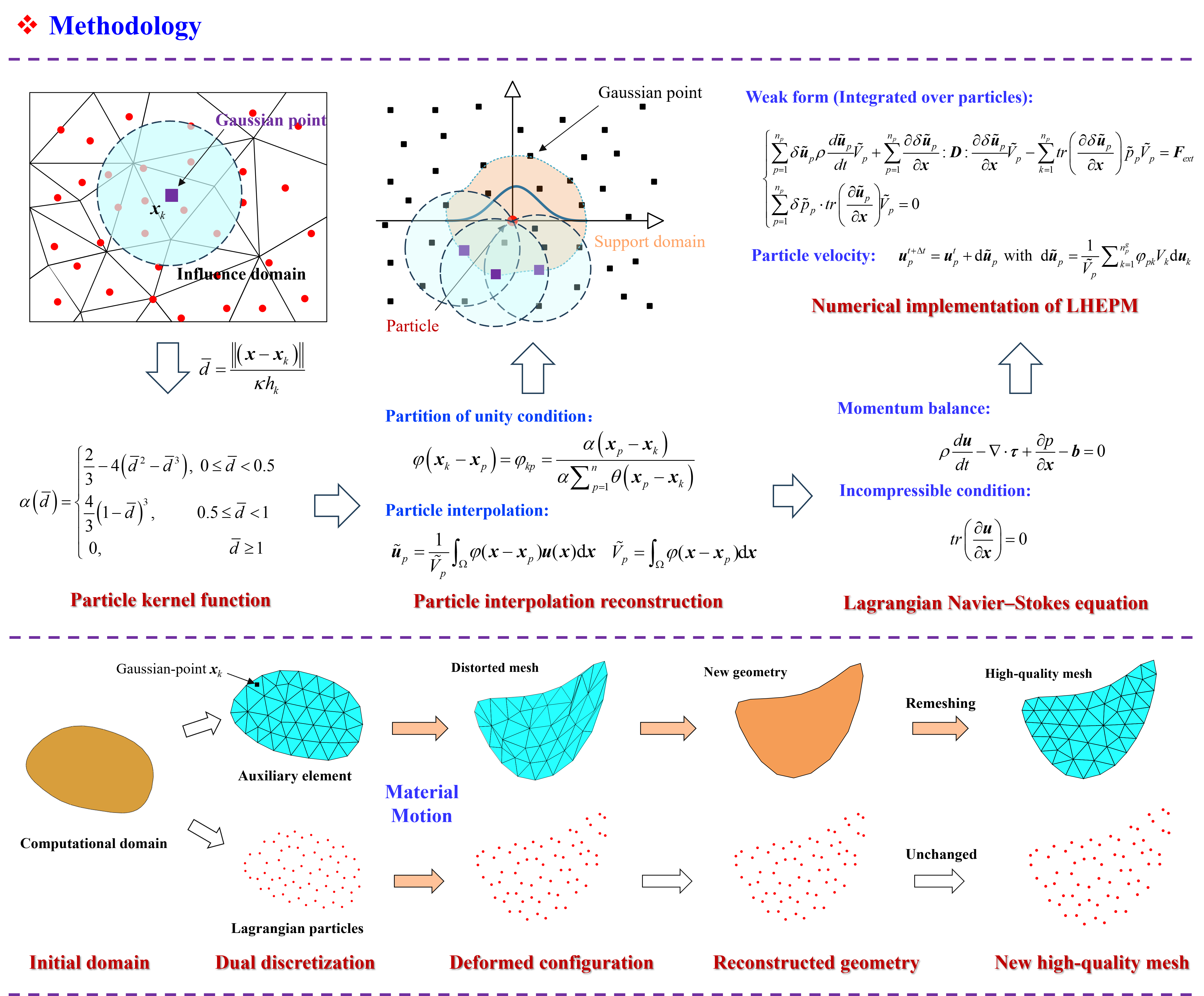
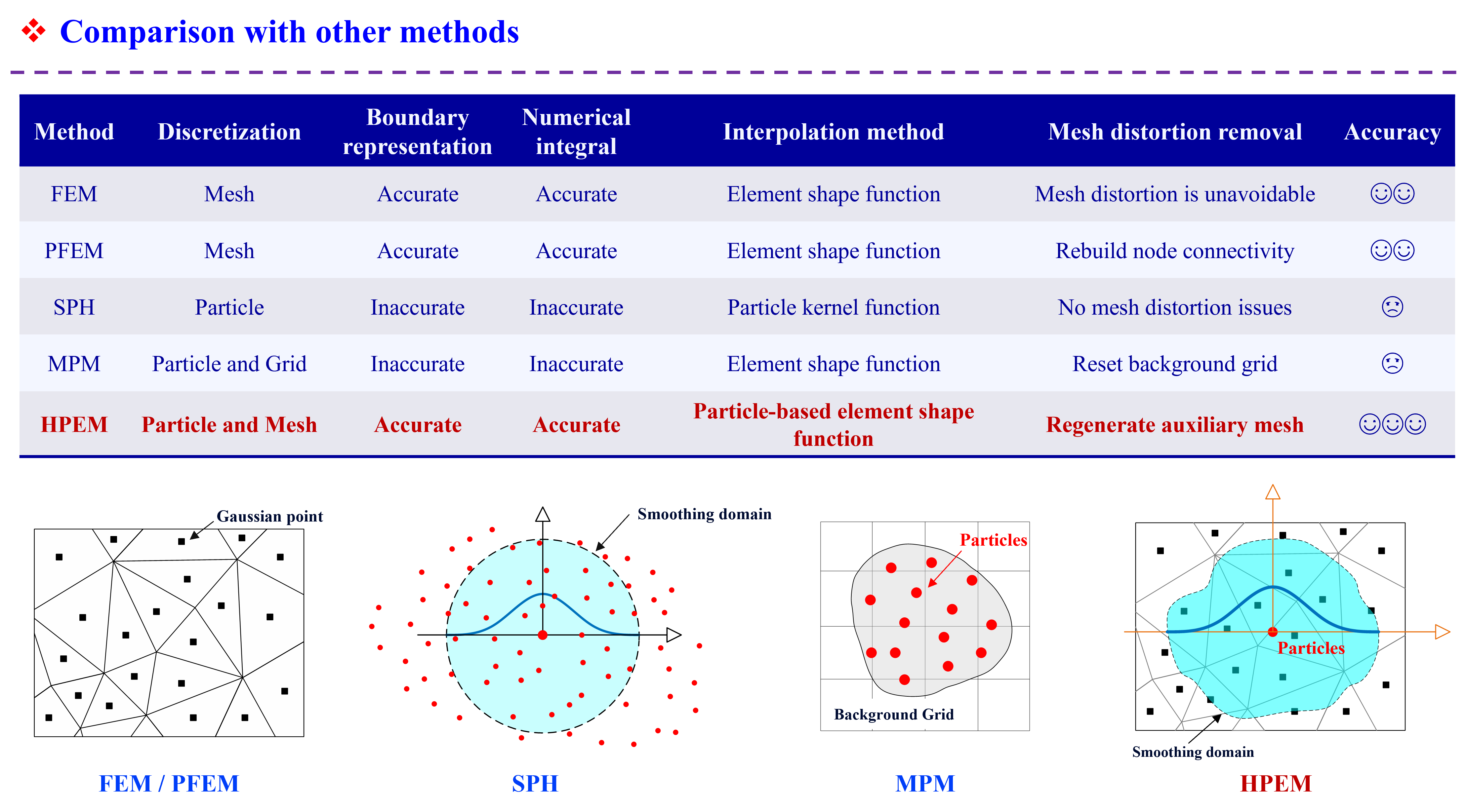
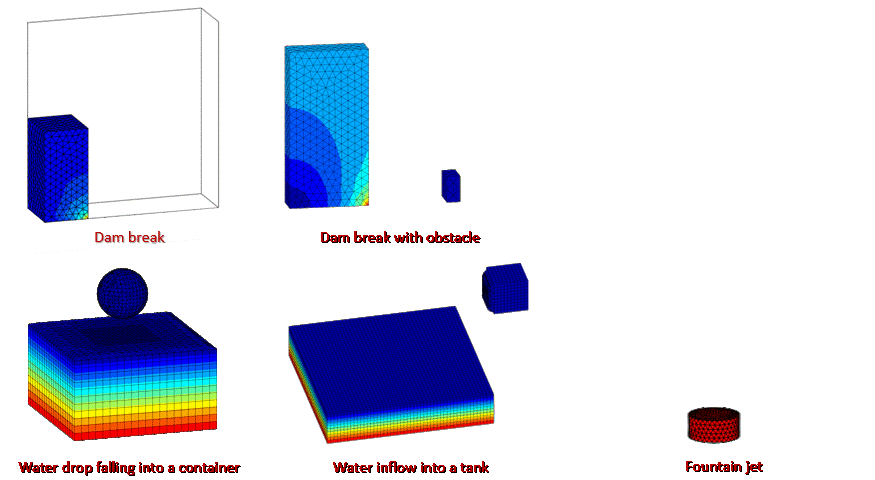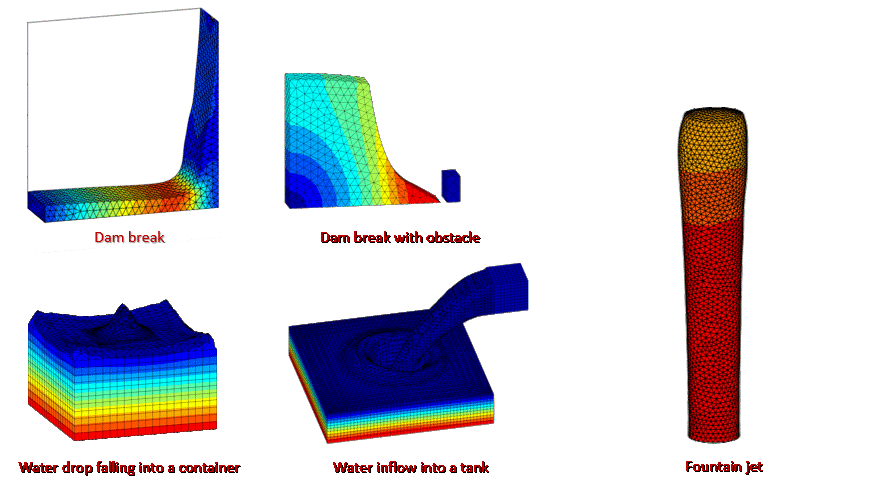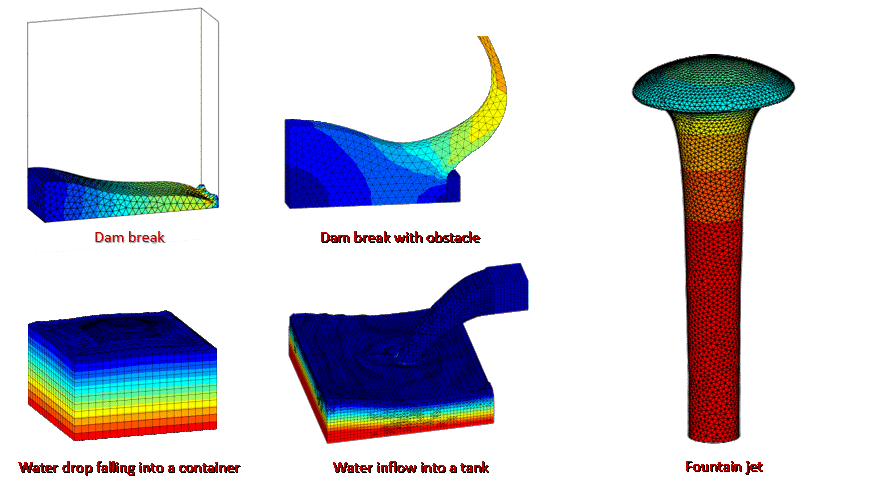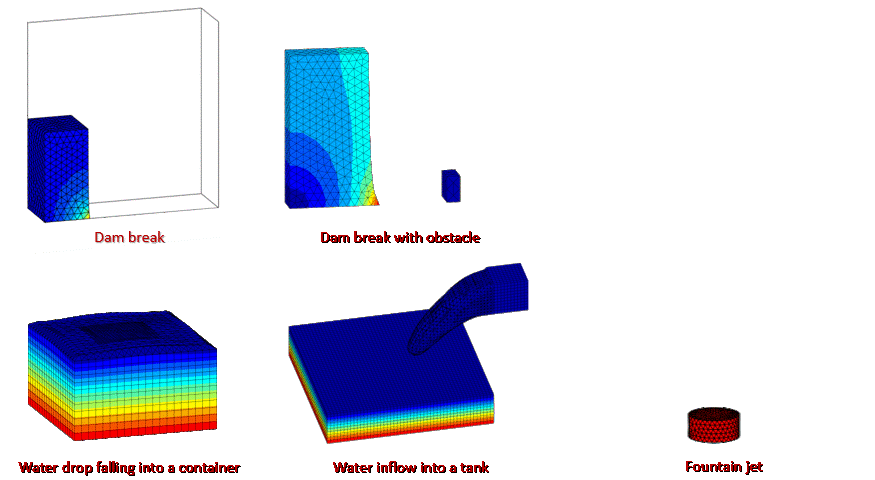
Abstract: Traditional numerical approaches for solving incompressible fluid dynamics problems face notable limitations, including convective instability and interface tracking in Eulerian approaches, severe element distortion in Lagrangian mesh-based methods, and reduced computational accuracy in particle-based approaches. To overcome these challenges, this paper develops a new Lagrangian Hybrid Element Particle Method (LHEPM) that combines two discretization schemes: underlying elements and material particles. The underlying elements, designed without storing historical variables, can be dynamically regenerated during the computation. These elements serve as temporary tools for discretizing physical fields within the computational domain, with their spatial interpolation subsequently reconstructed onto the particles via a kernel function. The proposed framework permits the seamless incorporation of various finite element techniques without requiring modifications, such as boundary condition enforcement, contact algorithms, and pressure stabilization. The effectiveness and performance of LHEPM are validated through its application to several standard fluid problems. Compared to other state-of-the-art methods, the proposed LHEPM avoids the need for complex treatment of convective terms and free-surface tracking typically required in Eulerian mesh-based approaches, such as the finite volume method (FVM); its unique interpolation technique and optimal particle integration enable significantly higher accuracy than particle-based methods like Smoothed Particle Hydrodynamics (SPH); dynamic mesh regeneration further resolves the mesh distortion issues inherent in traditional Lagrangian finite element method (FEM), making the proposed method a precise, efficient, and robust framework for incompressible fluid dynamics simulations.